In my last post, I made an extended analogy between today’s ed tech and 19th Century medicine. My core argument was that effective ed tech cannot evolve without a trained profession of self-consciously empirical educators any more than effective medication could have evolved without a profession of self-consciously empirical physicians.
In this post, I’d like to go beyond analogies and look at the actual state of some cutting-edge cognitive science. I want to do this for several reasons. First, a lot of educators are skeptical or even cynical regarding the potential relevance of this work to the ways that they think about teaching. This is completely understandable, particularly given that most educators hear about this sort of research through product commercials or hyperbolic media puff pieces. By exploring the science in some detail, I want to show that having a basic understanding of even foundational research that has no direct classroom applications can stimulate the thinking of classroom educators in useful ways.
Second, I want to show that even educators with no background in science or math can achieve an empowering level of cognitive science literacy with a reasonable investment of time (like the time it takes to read a long blog post, for example).
And finally, I want to show that, after we strip away the hype and the ennui it engenders, we can recover a sense of wonder about the science while maintaining a sense of realism about its practical applicability. I have chosen to characterize the methodological paper I’ll be explaining as an attempt to create a “microscope of the mind.” That’s dangerously close to “robot tutor in the sky that can semi-read your mind” territory. I hope to demonstrate that there is a non-hyperbolic sense in which we can believe that my microscope of the mind analogy is a reasonable one.
Here’s how I’m going to do it:
I am going to explain a research study on cognitive neuroscience. It’s not a big, sexy paper that gets coverage in outlets like Wired. It’s a methodology study. I’m going to explain enough of the basic underlying concepts in math, physics, and cognitive psychology for you to be able to get the gist of the paper and judge its significance for yourself. I’m going to explain how fMRIs work and what machine learning is. And I’m going to explain the larger context of why the researchers tried this particular experiment and how it is relevant to our larger understanding of how people learn. Along the way, I will touch on topics as diverse as theology, Russian literature, and the miracle of selfies, but always with the goal of showing how the science can be accessible, interesting, and relevant to non-scientists.
This is not a short read, but I hope that it will reward your effort.
A Theory of the Mind
The paper is called “Hidden Stages of Cognition Revealed in Patterns of Brain Activation” by John R. Anderson, Aryn A. Pyke, and Jon M. Fincham. Anderson is something of a legend in cognitive psychology circles. He rose to prominence in large part due to his ACT-R theory of the mind. This paper builds on that theory.
The first thing to know about ACT-R is that it’s not the kind of scientific theory that can be summed up in a pithy formulation like “things in motion tend to stay in motion.” It is a sprawling and hugely ambitious model that attempts to represent how human cognition works. We will dip our collective toe in the ACT-R water, but you should know that it is a deep well.
It is also relatively new and has not yet been universally accepted within cognitive psychology circles. The word “relatively” is critical because non-scientists tend to have a romanticized view of how long it takes for scientific consensus to emerge, particularly around complex or paradigm-changing theories. The clichéd “Eureka!” moment is usually only the first step down a very long road. Think about ACT-R on the same sort of time scale as I described for germ theory in my previous post. It took the scientific community more than 200 years to go from Antonie van Leeuwenhoek’s first observations of “animalcules” through a microscope to the universal acceptance of the germ theory of disease. That is the yardstick by which we can measure ACT-R as “relatively” new, given that the earliest version of it was articulated in 1973. Anderson and his colleagues have been accumulating evidence and refining the theory for over 40 years. Their work is well known and well regarded for a reason. But good science takes time, and building scientific consensus takes more time.
One reason that ACT-R is relevant to education today is that it has been very influential in promoting the development of what we commonly (and often sloppily) refer to as “adaptive learning.” Although most of the adaptive learning products on the market today are not based on ACT-R, the research conducted by Anderson and some of his former students has played a major role in spreading the general idea of adaptive learning.
But that wasn’t the research team’s original goal. In the 1980s, Anderson and his colleagues began building what they called “cognitive tutors” not as educational products but as experimental aids to help them test their theory of learning. Thirty-odd years later, they are experimenting with fMRI for similar reasons.
In order to truly understand the research goals and their relevance to education, both then and now, we need to understand a little more about the theory.
A Theory of Learning
The ACT-R model claims that we have two kinds of knowledge: declarative and procedural. Knowing-that and knowing-how. It also holds that we learn the knowing-how part by processing our knowing-that information with a particular goal in mind. For example, I know some things about the making of scrambled eggs. I know that you have to get rid of the egg shells. I know that “scrambled” means mixing up the insides of the eggs until they are blended together. I know that you make the scrambled eggs edible by heating them in a pan. According to ACT-R, these facts are stored in my mind as just that: facts. In order to actually make scrambled eggs, I have to go through the mental work of assembling them into a procedure. I need to create a recipe.
Here’s one that I might come up with (which I actually cribbed from a recipe on the web):
- Break some eggs into a bowl.
- Whisk the eggs until the whites and the yolks are thoroughly mixed.
- Put the eggs with a pat of butter and (optionally) some cheese into a skillet at medium heat.
- Keep stirring the eggs with a spatula until they reach the consistency that you like.
For a lot of people, this recipe would be straightforward. But not for me. I’m stuck on Step 3 because I don’t know what “medium heat” means in practice. We have a cheap old gas stove that doesn’t have clear settings on the knob. You have to judge the heat level from the flame level. What does “medium heat” look like? Do I wait until the pan is hot? How will I know when it’s hot enough? How will I know if it’s too hot? I don’t know how to plan to solve my scrambled egg problem. I’m missing some critical knowhow that I’m not going to acquire until I actually set out to cook.
It turns out there are steps involving the heating of the pan that may be invisible both to me as the novice and to the (presumably) expert cook who wrote the recipe. But for different reasons. They are invisible to me because I don’t know what I don’t know. I may be stuck on heating the pan, but that doesn’t mean that I know I’m stuck. Maybe all I know is that my eggs keep coming out badly. I may not be aware that the heat is the problem. On the other hand, maybe it was invisible to the expert because heating a pan is something so fundamental to cooking anything in a pan that she didn’t even think about it as something that needs to be learned.
Here’s Carnegie Mellon University professor (and Anderson’s former student) Ken Koedinger talking about this problem:
[https://youtu.be/THe7epRHPUM]
If you’ve taught, then maybe this sounds familiar to you. A student gets stuck and it takes some real work to figure out why. Sometimes you don’t figure it out. Sometimes you realize there’s a connection they are missing that you take for granted or you thought you covered clearly in class. The method that Koedinger uses in his own class is a simple empirical approach that many educators could use to improve their own teaching—if they think about part of their job as uncovering stumbling blocks that might normally be invisible to them as experts.
But even that only solves part of the problem, because even if you did cover the connection in your lecture, that may not have helped the student. ACT-R suggests that we only learn the knowhow by actually doing something. In other words, you can watch a YouTube video of somebody scrambling an egg, but all that gives you is knowing-that knowledge. The only way to truly learn how to cook is by cooking, just as the only way to learn how to write is by writing and the only way to learn a language is by speaking or reading it. Even had somebody provided me with a better explanation of what “medium heat” means, I would still need to learn how to put the idea to practical use given different stoves, different pans, and so on.
If you believe in the constructivist teaching philosophy, then this view of how learning works may sound less foreign than you expected. ACT-R holds that learners have to construct certain kinds of knowledge themselves and that their goal for doing so is integral to the learning process. But how do students construct that knowledge? Where—and why—are they likely to get stuck on certain steps for different subjects in different learning contexts?
Early cognitive tutors were essentially tools for creating different experimental conditions under which researchers could test both whether their “missing steps” theory was correct and also to test whether specific hypothesized missing steps in specific kinds of problem solving were, in fact, missed by the students.
Separating the Research from the Hype
Cognitive tutor research proved very successful at identifying gaps in procedural knowledge and showing how remediating those gaps could improve student performance for knowledge domains that are formally and straightforwardly procedural, like math and computer programming. And that’s roughly where adaptive learning products are stuck today, whether or not they are based on ACT-R. They are generally good at identifying and remediating gaps in students’ procedural knowledge for relatively formal procedural subjects, particularly math. There’s a second, separate strain of adaptive learning products that are good at ensuring that students are able to commit declarative knowledge—facts—to memory. But in either case, the practical applications of adaptive learning thus far have largely been remediation within a fairly narrow range of basic learning problems.
This where my analogy to medicine invites misunderstanding. Our current system of medicine in the United States (and much of the world) is focused on treating sickness, which could be seen as analogous to remediation. It’s focused on fixing something that’s broken. When educators hear talk of “efficacy” and see the current state of adaptive products or retention early warning systems, it’s easy for them to think that an analogy to medicine means focusing on “fixing” what is “broken” in the student. But the emphasis on sickness in our medical system, which is shaped by business models, insurance regulations, and all sorts of social and legal conventions, is separable from the broader idea of medicine as an applied science. We could imagine a different system drawing from the same science that emphasizes teaching people how to improve their own wellness.
Similarly, the ACT-R theory has much to say about growing from being a novice who struggles to interpret recipes to an expert chef who creates her own recipes. It’s about building up more sophisticated procedural knowledge—more knowhow—through practice.
Conceptually, this idea applies to a subject like writing as well as it does to math. In the early stages of writing, students learn basic procedures—how to use punctuation, how to form a complete sentence, how to form a coherent paragraph, how to string paragraphs together into an argument, and so on. But as they get more practice, their writing production models get more sophisticated. Knowing about semicolons is a little bit like knowing about medium heat. Understanding the concept is relatively straightforward. Learning how to use semicolons effectively in different situations to impact the tone and readability of your writing takes time and practice. Good writing teachers understand this progression, sometimes instinctively, and scaffold the skill-building activities accordingly.
In theory, ACT-R should have as much to say about how intermediate writers become more sophisticated in their use of punctuation as it does about how math beginners can learn how to calculate the slope of a line. In practice, studying how people learn to write, or reason critically, or paint, or perform any number of complex skills that are not formally procedural, is incredibly hard. Arthur C. Clarke famously wrote, “Any sufficiently advanced technology is indistinguishable from magic.” The same could be said for any sufficiently complex thought or learning process.
That’s why researchers like John Anderson are reaching for new tools like fMRI. They need new ways to tackle this incredibly hard problem.
What “Building a Microscope of the Mind” Would Mean
Let’s accept for the sake of argument that the parts of ACT-R I described in the last section accurately reflects the way we learn to perform all sorts of complex thought work. If so, then any learning process under that umbrella would have some common, recognizable moments, regardless of the content being learned. Here are a few:
- The moment that you recognize what kind of problem it is (e.g., a scrambling-an-egg problem or a persuasive argument problem)
- The moment when you apply the steps that you think will solve the problem (e.g., put the eggs in a skillet at medium heat)
- The “uh oh” moment when you realize that your steps aren’t working (e.g., you don’t know how to tell whether the pan is at medium heat.)
These moments, these steps along the way, could be collectively thought of as a general learning mechanism that learners recruit and modify as needed when learning all kinds of things. If so, then maybe we could see signs of that mechanism at work in the brain.
Imagine that we could fashion an instrument to “see” those moments. I’m not talking about a mind-reading machine out of the movies where the contents of your thoughts are projected on a video screen. I just mean that we could see a blip of brain activity that reliably corresponds to an “uh oh” or “ah-hah!” moment, for example. If we could see evidence of particular moments in the learning process, some of which may be unconscious in the learner, then we might be able to get just a little more insight into how the mental magic works.
This wouldn’t mean that all the deepest mysteries of the human mind would suddenly be revealed to us. Remember, it took several hundred years to get from Leeuwenhoek seeing bacteria to understanding how disease gets transmitted. And I suspect that devising and proving a theory of learning is at least an order of magnitude more complicated that doing the same for a theory of disease transmission. We may never understand it all. But if learning works roughly the way ACT-R hypothesizes that it does, and if those general steps of learning reliably correspond to certain activities in the brain, and if we can reliably observe those activities while also observing the person in the act of learning, then we could be able to “see” their train of thought unfold inside their heads in a very real, albeit crude, sense.
Over a realistic time scale of decades or centuries, such a microscope of the mind could enable research that leads to real breakthroughs in understanding, just as Leeuwenhoek’s technological toy—which he originally invented to be able to see threads better to help his cloth business—enabled ground-breaking research in medicine and other fields that eventually changed the world. Science is all about following a long chain of “ifs”, merging with other long chains of “ifs” over time, like tributaries merging into a river.
But is it even possible to build such a device? This is the question that Anderson and his colleagues set out to answer in their methodology paper. And as with germ theory, their work is built on top of several different strands of math and science built over the last century and a half. We’re going to need to understand a little bit about those strands before we can understand their work, starting with fMRI research.
What an fMRI Does
While there are a few different brain tools that are available for researchers looking to study brain activity, the fMRI has been all the rage in brain studies for a while now. The popular narrative is that these giant, expensive, and complicated machines can actually see our minds at work. That they can reveal our innermost thoughts and beliefs, casting them up on a screen for all to see.
The truth is a lot more complicated. MRI, or Magnetic Resonance Imaging, is based on some very complicated math and physics, but the core principle is something you were probably exposed to in middle school. At some point in your science schooling, you likely conducted an experiment with a magnet and some iron filings, where you got to see the filings align with the magnetic field.
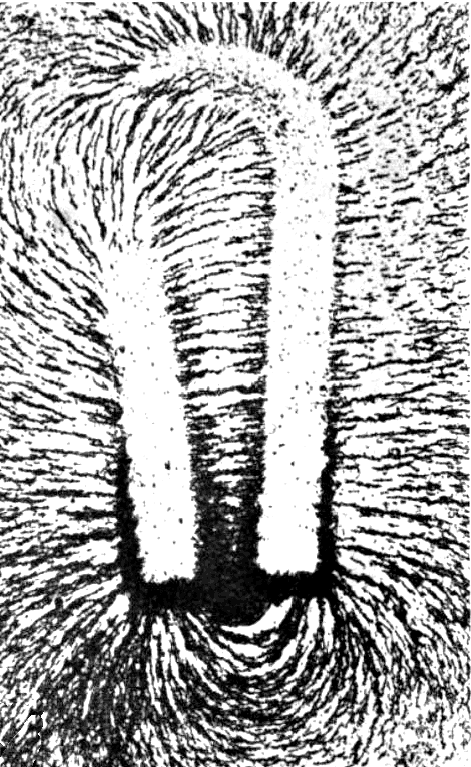
The heart of an MRI is a giant magnet roughly a thousand times more powerful than the ones you probably have on your fridge. The nuclei of many common molecules in your body, such as the iron in your red blood cells and the water throughout your body, respond to a strong magnetic field by aligning themselves with it, just like the iron filings did in your middle school experiment. When that field is turned off, the nuclei return to their natural alignments. In doing so, they give off their own miniature magnetic fields—magnetic resonance—which the machine can pick up and measure. Crucially, different tissues return to “normal” at different rates. Through some very complex calculations, the machine sifts through all these different magnetic fluctuations and converts them into a three-dimensional map of “voxels” (which are the 3D versions of pixels).
It’s an incredibly clever application of physics that’s really good at providing images of bones and tumors and other structural features. But we want to observe thought. How could that work?
The short answer is “very indirectly.”
An innovation to MRI technology called Functional Magnetic Resonance Imaging, or fMRI, can detect the difference between oxygenated blood flowing into a part of the brain and deoxygenated blood flowing out of a part of a brain. The difference shows us where oxygen is being consumed in the brain, presumably to fuel neural activity.
This approach has a lot of limitations, some of which are obvious and some that are less so:
- We don’t fully understand how blood flow actually relates to what’s happening in the cortical neurons.
- For that matter, we don’t really understand how the neurons “compute” or “think.” We also don’t know whether thinking is truly and entirely electrical or whether it happens entirely in the brain.
- fMRI is slow. Its temporal resolution—the amount of time it takes to construct one image—is measured in seconds. But thought processes often occur over milliseconds. It’s little like a camera aperture setting.1 An fMRI needs a slow setting to capture the subtle information it is trying to get, like the setting on your camera that you might use to take a picture of a landscape at sunset. But that setting is not good for trying to get a shot of a racehorse running down the home stretch.
- The science and technology are both incredibly complex, to the point where mistakes are hard to identify. To give one high-profile example, there was a bug in one widely used fMRI software module that went undiscovered for 15 years and may have invalidated thousands of brain studies as a result.
- The whole idea of visualizing something functional (like thought) using a device intended to observe something structural (like a tumor or a broken bone) assumes that structure and function are closely correlated. But the areas of the brain that appear to be associated with specific memories or higher thought processes vary considerably from person to person. Trying to find patterns that account for this variability is difficult.
These are all known problems but not solved problems. fMRI is incredibly advanced technology, but it is also extremely crude if your interest is not in how brains work but in how thinking works.
To compensate for the limitations of fMRI, Anderson and his colleagues turn to another trendy technology that is often sloppily and irresponsibly characterized in popular media: machine learning.
How Machine Learning Works
For most of its existence, MRI has been optimized to work well with one very particular type of information processing system: the human visual cortex. It makes pictures of our insides that we can understand with our eyes. That makes sense if we want to see where a tumor has spread or whether a disc in the spine has degenerated. But it’s not the best method for detecting the kinds of patterns that Anderson et al. want to see. Machine learning provides some alternates that are better suited to the purpose.
The term “machine learning” is a misleading misnomer that invites hype. Machine learning can best be thought of as a family of statistically based scientific methods that are applied using the brute force of a computer. In other words, it’s based on the idea that if we perform the right kind of statistical analysis of enough examples, that analysis will reveal patterns, including ones we might not have caught using our direct observational skills.
Let’s say you want to reliably identify email spam so you can unclog your inbox. You observe certain features that are more or less common to emails that you think of as “spam.” If it has the word “viagra” or “cialis” in it, it’s almost certainly spam. If it has links to a URL with a Czechoslovakian domain, there’s a good chance that it’s spam. If it has the word “lonely” in it, it might be spam. And so on. If you are mathematically inclined (and maybe a little obsessive), you could come up with a formula that assigns a probability that a given email is spam based on various features like word choice, punctuation, hyperlinks, whether you’ve ever replied to an email by the sender, and so on.
But you probably wouldn’t get the formula perfect the first time. For example, you may guess that 7 out of every 10 emails with bad punctuation in them are spam. But in your heart of hearts, you know that’s a guess. Maybe you’re…say…sixty percent confident that your guess is right.
So, if you’re proficient in a branch of math called Bayesian probability, you would plan to adjust your formula based on patterns observed in each example that comes in. For example, suppose you get a lot of emails from teenagers in your family who use too many punctuation marks in some places and not enough in other places. As a result, a couple of emails from your nephew get rated as spam by your formula. But you planned for this. You’re formula has a little loop in it that adjusts how heavily it counts punctuation every time it gets corrected. If you applied the formula to a few thousand email messages in succession and adjusted it each time, it would eventually get pretty good at matching your idea of what counts as spam. But that would be tedious. So you could write a computer program to do it for you instead. Every time you correct its spam judgment, it runs a little loop to change the increments on its various spamminess predictors. Eventually, it gets pretty reliable without a whole lot of oversight from you.
This is called “machine learning” because you are not tweaking the algorithm—the formula—every time a new message comes in. You are not writing new explicit rules for how to judge the spamminess of a message. Instead, you’ve written meta rules that tell the machine how to adjust the formula itself based on some very basic input from you. Every time you rate an email with bad punctuation as “not spam” the loop in your program adjusts the amount of weight it puts on bad punctuation by a pre-defined increment. The machine is “learning” in the sense that it is getting better at identifying the complex patterns of features that fit the range of emails that you think of as spam without you telling it exactly what it got wrong every time.
If you had enough foresight in how you wrote your formula, it may even “learn” to detect patterns of spamminess that wouldn’t have been obvious to you. For example, it might find that most of the messages you identify as spam come in the middle of the week, which is something you might not have noticed when just deleting spam from your inbox on your own. But your program would only find that pattern if you thought to include “day of the week” as one of the factors that your formula analyzes. The magic is in the design, which is a statistical analysis method devised by a human.
The critical corollary to this point is that, whenever somebody tells you that a research method (or a product) works through “machine learning,” they mean it does its work through a specific procedural method that was written by humans who had certain ideas and assumptions about how large quantities of information could be analyzed by looking for specific kinds of patterns in specific ways. It is not a magic wand. It is a scientific method. One that can be understood and interrogated.
Anderson and his colleagues use two different kinds of machine learning in their attempt to overcome the limitations of fMRI. One of those methods has become increasingly popular in fMRI research while the other is relatively novel to the field (though widely used elsewhere). We’ll need to understand both approaches to understand the paper, starting with the one that is more widely used in fMRI research.
Understanding Multi-Voxel Pattern Analysis
As fMRI researchers wrestled with some of the limitations of the technology, they realized that machine learning techniques could be helpful in recognizing patterns that may not be obvious to the human eye, just as a Bayesian spam filter may pick up patterns that aren’t obvious to the person who is receiving the spam. It’s pretty easy to imagine how that training might work:
Machine: Is this brain image of a person looking at an apple?
Scientist: Yes.
Machine: How about this one?
Scientist: Yes.
Machine: And this one?
Scientist: No, that brain image is of a person looking at a shoe.
…
Machine: I see an 83% correlation with low but detectable levels of activity in these 4 areas of brain images of people who are looking at an apple, but only an 11% correlation of similar activity in brain images of people looking at shoes.
This family of machine learning techniques is called “Multi-Voxel Pattern Analysis (MVPA)”. It is used by cognitive scientists to create a fingerprint of brain activity that is distinctively correlated with a particular mental state. MVPA has proven to be shockingly good at “seeing” visual processing in the brain, particularly keeping in mind all the limitations that we know about how an fMRI machine works. For example, researchers at the University of Oregon developed a way of reconstructing faces people were looking at based on their fMRI data. The images aren’t good enough that you would say you could immediately recognize each face, but they are certainly recognizable as faces.

That’s pretty amazing, given that it’s deduced from data about the magnetic fields generated by individual blood molecules flowing through brain while the experimental subject was looking at the face. It shows that, for at least some mental processes, we can use a combination of fMRI data and specific machine learning algorithms to identify a fingerprint of brain activity that corresponds to very specific information about the content of a mental state.
Anderson and his colleagues hoped that MVPA could solve at least one of their research problems. If they could develop fMRI fingerprints associated with ACT-R hypothesized mental states, then they would be on their way to being able to “see” thought.
But they had another problem to solve before they could cross the finish line. An image in the mind of an apple or a face is a single mental state. The researchers wanted to observe a multi-state mental process involved with solving a problem. And remember, fMRIs have lousy temporal resolution. An experimental subject can stare at an apple for as long as the fMRI needs to run. In contrast, a person solving a math problem may have already gone through some or all of the stages of their thought process in the second or more that the machine needs to construct a single image. The team needed a way to tease out the differences in the hypothesized mental states given their highly imperfect instrument.
So they turned to another machine learning-based scientific method called “Hidden Semi-Markov Models (HSMMs)”.
Understanding Markov Chains
As I said earlier, machine learning is essentially the brute force application of a statistical pattern matching method over many examples. In this case, before we can really understand how the HSMM machine learning algorithms work, we have to understand a little bit about the mathematical intuitions that underpin them. Before you can understand Hidden Semi-Markov Models, you have to understand a little bit about Markov chains.
The intellectual history here is fascinating. In 19th-Century Europe, but particularly in 19th-Century Russia, an intellectual debate raged that still continues to this day in some surprisingly familiar quarters. The Enlightenment thinkers believed that all problems of humanity and all mysteries of the universe would eventually yield to the cool light of reasoned inquiry. This specifically included the laws of human behavior.
Not everybody loved this idea. For example, Dostoyevsky wrote in Notes from the Underground,
Indeed, if there really is some day discovered a formula for all our desires and caprices – that is, an explanation of what they depend upon, by what laws they arise, how they develop, what they are aiming at in one case and in another and so on, that is a real mathematical formula – then, most likely, man will at once cease to feel desire, indeed, he will be certain to. For who would want to choose by rule? Besides, he will at once be transformed from a human being into an organ-stop or something of the sort; for what is a man without desires, without free will and without choice, if not a stop in an organ?
Some of you may feel a similar angst right now reading this post. The idea that our thoughts can be predicted, that we can somehow be dissected and reduced to an algorithm that can be seen running in our brains, is a profoundly uncomfortable one for many people (including me). How can we reconcile the idea that humans follow certain laws with the concept of free will? How can we simultaneously believe in student predictability and in student agency?
Believe it or not, this is a question that deeply concerned mathematicians in 19th-Century Russia. One in particular. Pavel Nekrasov, a theologian turned mathematician, was extremely interested in the concept of free will. Specifically, he was for it. He believed that God gave humans the ability to make their own choices for good or evil. And he saw a connection between that belief and mathematics. In his view, if humans truly have free will, then their behavior should share certain characteristics with randomness. Just like the likelihood of a coin flip coming up heads or tails is completely independent of the results of any previous coin flips, the likelihood of a person making one decision should be independent of other decisions. Each time we decide, we choose our own destiny afresh. Likewise, groups of humans should not be predictable, since each one has free will and is not bound by any laws of human behavior. Nekrasov therefore wanted to show that human behavior looks mathematically random.
One of the best indicators of randomness that was known at the time was something called the law of large numbers. It’s a pretty simple and intuitive concept. If you flip a fair coin an infinite number of times, how often will the coin come up heads? Roughly half of the time, right? Even if you get a streak of heads or a streak of tails, if you keep flipping the coin enough times, the results will converge on the odds. If you took an ordinary six-sided die of the kind you’d use in a craps game and rolled it an infinite number of times, how often would the die come up a six? Roughly one in six times. The law of large numbers says that, over an infinite number of trials, the results of random acts tend to converge on the expected odds.
“Aha!” thought Nekrasov. Many of the early sociological studies of the time, such as crime statistics, were returning results that appeared to conform to the theory of large numbers. They looked random in that way. Nekrasov asserted that because these human decisions appeared to conform to the law of large numbers, they must also be independent from each other in the same way that one coin flip is independent from the next.
His contemporary, a curmudgeon by the name of Andrei Markov, didn’t like that idea at all. Apparently motivated largely out of spite, he wrote a paper in 1906 to refute Nekrasov’s contention. He showed that successive actions can appear to conform to the law of large numbers and still have one trial be influenced by the previous trial.
The precise details of the paper don’t matter for our purpose, but one key concept does. Along the way to publicly humiliating his rival, Markov came up with an idea that is now called the Markov chain, which extended our understanding of statistical probability beyond isolated independent events.
You don’t need to understand the math to grasp the underlying intuition. Suppose I asked you the following question:
Which consonant is less likely to be followed by another consonant: An “s” or an “r”?
After thinking about it a little, you would probably say an “r”. There is still an element of unpredictability. If you were playing “Wheel of Fortune” and you saw that the first letter of a word was “r”, you wouldn’t automatically know what the next letter is. You might realize there’s a small chance that it could be an “h”. But you’d also know that it isn’t a “q” or a “c”. The probable value of one unit can be influenced by the previous unit.
Markov thought up this kind of relationship to provide an example of a dependence between discrete actions that could nevertheless appear to conform to the law of large numbers. But again, you don’t need to understand the math. If you got the “Wheel of Fortune” part, that’s all you need to know for our purpose.
While Markov’s first paper didn’t talk about consonants and vowels, sticking strictly to math examples, he wrote another paper a few years later using Markov chains to analyze Alexander Pushkin’s literary masterpiece Eugene Onegin. He showed the degree to which the Russian language violated the principle of independence, which is another way of saying he showed the degree to which the written Russian language is predictable.
This core intuition about predictability and randomness not being completely binary and oppositional is helpful in several ways. First, it may give us at least a glimpse of a way out of our metaphysical quandary. There is a sense in which Markov’s paper showed the degree to which Pushkin’s poetry is predictable. But not a sense that diminishes the author’s artistry in any way. Perhaps we’ll find similar balances in cognitive science.
More immediately, Markov applied a brute force statistical technique to determine the degree to which non-obvious patterns in a sequence are predictable. Even in a poem. This is exactly the kind of approach that is amenable to machine learning. It also has the seeds of what Anderson’s team needed to identify a sequence of brain patterns rather than a single one.
We’re almost there now. We need to make just one more stop on our intellectual journey before we have all the concepts we need to understand the research paper. We just need take the step to turn Markov chains into something useful in our quest for a microscope of the mind.
Understanding Markov Models and Information Theory
Like Nekrasov, American engineer and mathematician Claude Shannon was interested in the relationship of randomness to a seemingly unrelated big idea. But rather than free will, Shannon was interested in information value. If a new piece of information could not be predicted based on previous pieces of information, then it must be entirely novel. On the other hand, if the new information could be made any more predictable by knowing previous information, then that previous information in some sense contains information about the piece that comes next. Knowing that the first letter of an English word is “r” means that I also know the next letter is not “q”.
Being an electrical engineer interested in communications technologies, Shannon saw some immediate practical implications. First, he was able to figure out how to cram as much information into as few bits—a computer term invented by Shannon—as possible.
Suppose I write a sentence like this:
Mr. Rogers’ Neighborhood was truly wonderful show.
You would still know what the sentence means even though I left out the “a” between “truly” and “wonderful”. Heck, you might not even notice the dropped “a” if you read it quickly. You can decode that sentence just fine without the article.
Now let’s drop all the vowels in the same sentence:
Mr. Rgrs’ Nghbrhd ws trly wnderfl shw.
That’s harder, but you can still make it out.
Shannon worked out how to find the smallest package of symbols necessary to convey the information you want to send. In other words, he came up with the math that makes image and sound compression (among other things) possible. The next time you send a selfie from your mobile phone or stream a movie over Netflix, you’ll have Claude Shannon to thank for it.
The flip side of this innovation is that he also figured out how to recover lost information from a noisy signal. Whether the challenge was being able to hear and understand a voice that was transmitted through a cable that ran all the way across the bottom of the Atlantic Ocean or getting the crucial details of an encrypted war-time radio message sent from a ship in stormy seas, extracting lost signal information was the order of Shannon’s day. He figured out that we can use the same basic principles that let us strip out unnecessary bits of information to recover lost ones. When you read the sentence without the vowels, you are able to fill the vowels in. Likewise, when you are talking to a somebody over a bad cell phone connection, you can often make out what they are saying to you even if some of the words are inaudible. Shannon’s information theory is a mathematical formalization of this common experience. He built on the idea of Markov chains to figure out how to recover lost parts of a signal.
Since then, statistical methods built on this approach, called Markov models, have been used in a huge and ever-growing range of applications. For example, they’ve been very important in solving speech recognition problems. Between regional accents, individual idiosyncrasies of speech, background noise, and uneven phone signals, getting computers to understand human speech has been a huge challenge. Again, without having to know the mathematics, you can probably get a sense of how Shannon’s and Markov’s intuitions could be used to fill in missing portions of a sequence that are lost to noise. The Hidden Semi-Markov Model that Anderson and his colleagues used is just a particular variant designed to account for the particular characteristics of the lost or missing parts of the (thought) sequence they were trying to recover in their experiment.
Understanding “Hidden Stages of Cognition Revealed in Patterns of Brain Activation”
We finally have all the tools we need to understand the paper.
Anderson and his colleagues believed they could use Multi-Voxel Pattern Analysis to identify the fingerprints of specific problem-solving steps in fMRI scans. They would use a Semi-Hidden Markov Process to find the boundaries between these mental states and fill in missing information caused by challenges such as the slow speed of fMRI imaging.
That paragraph you just read was short. But it requires a lot of context to understand. If you started reading this post without any of that context but found the paragraph to be even partly straightforward and comprehensible, then I hope you’ll take a moment to reflect on how much math and science you’ve been able to learn in the time it took you to read this far.
The method described in that paragraph is what the researchers wanted to prove could work. While they are ultimately interested in complex questions like how novice thinkers become expert thinkers, they first needed to test their crude “microscope” on something that would be easier to “see.” In this case, “easier” means a fairly course-grained process that is relatively slow. So instead of trying to detect the fine details of somebody struggling with a hard problem, they started by looking at the most basic steps of the problem-solving process.
At a high level, ACT-R theory proposes that there are four distinct stages of problem-solving: encoding, planning, solving, and responding. These terms are largely what you would guess them to be. Think about encoding and responding as input and output. If I’m asked to solve a math problem, the first thing I need to do is translate the math symbols on the page into something that makes sense to me. If you’re not a math person, you might think of this as decoding. But the idea here is that, whatever language the raw information is in, I need to translate it into…let’s call it the operating language of thought. If it’s a cooking recipe, I need to read the instructions and translate them into concepts that my mind works with natively.
At the far end of the process, after I’ve solved the problem, there is some work to do in order to get it back into the world. I might need to make my fingers work to type the answer, for example. That’s “responding.”
In between encoding and responding, I need to identify the strategy I’m going to follow—the mental “recipe”—and then do the mental work. First I recognize that this is a long division problem; then I divide. First I plan, then I solve. Together with encoding and decoding, these represent the high-level mental states that Anderson and his colleagues wanted to fingerprint in fMRI scans so that they could apply some basic measurements, like how roughly how long a subject spent in each state when trying to solve a given problem.
The researchers’ strategy appears to have worked. Using their method, they found that, for example, subjects solving problems that were hard to figure out spent more time in the planning stage while subjects solving problems that had lots of steps took more time in the solving stage. So at first blush, our microscope seems to be working.
Anderson and Jon M. Fincham conducted a follow-up study in which they used the same technique to study people who were consciously thinking through a new way to solve a problem when the method they had been taught didn’t work. In other words, they were trying to see the signs in the brain of people constructing new solutions to hard math problems. Once again, the researchers’ method seemed to work. They were able to identify and observe the markers of the steps ACT-R predicts that people have to go through when they learn.
Let’s review how all of this works from beginning to end:
- Some people place their heads inside a giant magnet.
- While they are solving math problems, the magnet fires up, realigning the nuclei in the blood flowing through their brains.
- The magnet then powers down.
- The molecules in the brain blood change their alignment back to their normal position, producing many tiny magnetic fields in the process.
- The machine registers those many magnetic fields and uses some extremely complex math to deduce spacial information about blood flow in the brain.
- The researchers apply some more complex math to identify particular patterns across different brains that represent individual steps in a thought process.
- Then they use still more complex math to confirm that the brains are going through those steps and measure the amount of time that they spend in each of those stages—even when their machine isn’t fast enough to catch each subject going through every stage.
- As a result of all of that, the researchers can actually detect the steps that our brains go through during the process of solving a problem.
I think it’s fair analogy to call their innovation a microscope of the mind. Crude, yes, but no less astonishing or impressive an accomplishment for it.
That’s pretty crazy.
Why It Matters
By reading this far, you’ve now made an investment in understanding some pretty heavy science and math, at least a conceptual level. What is the potential return on your investment?
Well, for starters, this method may become a lot more accessible to a lot more people. fMRI machines are expensive and therefore hard to come by. They’re also huge and uncomfortable for the subject to be in, which limits their applicability. Anderson is interested in whether the same technique can be applied using a technology called an electroencephalogram (EEG). EEG has its own limitations, but they are different from those of fMRI. In particular, it has two relative strengths that make it attractive. First, it has much better temporal resolution. It can detect changes that happen in the brain over milliseconds. Second, it’s vastly lighter and cheaper than fMRI, and getting lighter and cheaper all the time. There are even companies that sell simple EEG devices direct to consumers now. If the researchers are able to get their approach to work with EEG, it would become practical for many more research teams to run experiments like Anderson’s.
Take a moment and ask yourself this question: If you had access to these kinds of capabilities, what would you want to study? What learning moments would you like to see using this method that could help you teach a concept or skill more effectively? Or generally become a better teacher by understanding learning better?
More broadly, if educators understand some of the basics of the science that you hopefully understand now, they might ask questions like the following:
- Is this adaptive learning product a cognitive tutor based on the ACT-R model? (Try that one on your textbook sales rep. I dare you.)
- Can you give me some examples of the kinds of learning stumbling blocks that this product helps students with in my teaching domain?
- What is your research basis for knowing that the stumbling blocks you think you’ve identified are, in fact, problems?
- Can you explain to me in plain English the kinds of factors that this “machine learning” you keep talking about takes into account and roughly how the program uses new data from the students to adjust over time?
- When you talk about “brain science,” can you explain to me what that really means? What do you think you know about the brain, how do you know it, and how does that knowledge apply to the way that the product works?
Educators can learn to ask these questions and understand the answers without having to have a degree in statistics or neurobiology.
Beyond that, some knowledge of these techniques can be useful to scholars across a surprisingly wide range of academic domains. For example, here’s a paper about using Markov chains to confirm the authorship of (allegedly) Shakespeare’s Richard VI plays. Again, even if math and computer science aren’t your cup of tea, having the basic literacy to understand work being done in the digital humanities can be helpful to a humanities scholar. And it’s not as hard or scary as it might seem.
Finally, any instructor who takes her teaching seriously should be at least a little curious about the question, “How can the advances we are making toward understanding how brains and minds work stimulate my own thinking about how I work with my students?” As this blog post hopefully shows, answering that question is not as simple as reading a trade article or two. There is much to learn. Some of it won’t be obviously relevant or helpful, but since scientific discoveries build on each other, you can’t always know in advance which parts will eventually be useful. The best approach may be to cultivate your literacy in the research rather than to approach it as a case-by-case information-seeking problem.
Every good teacher that I have met is a curious person to some degree. There is a lot to be curious about here.
- For those of you who remember cameras. [↩]
[…] [Link] [Comment] Source: New feed2 […]